Lernauftrag 12: Logische Schaltungen vereinfachen
Hier findest du die Aufgaben ohne Lösungen.
Aufgabe 1
Die folgende Schaltung entspricht einem Logiksymbol.
Ermittle zuerst die Funktionsgleichung, stelle dann die Wertetabelle auf und gib schlußendlich das vereinfachte Schaltzeichen (Logiksymbol) an.
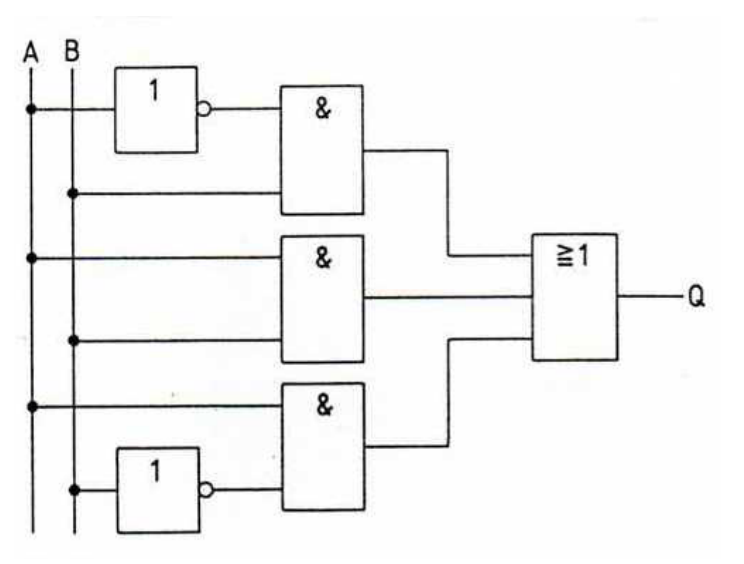
\(Q=(\overline A\land B)\lor(A\land B)\lor(A\land\overline B)\)
| B | A | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Vereinfachung: ODER
Schaltzeichen siehe Tabellenbuch S. 355
Aufgabe 2
Die folgende Schaltung entspricht einem Logiksymbol.
Ermittle zuerst die Funktionsgleichung, stelle dann die Wertetabelle auf und gib schlußendlich das vereinfachte Schaltzeichen (Logiksymbol) an.
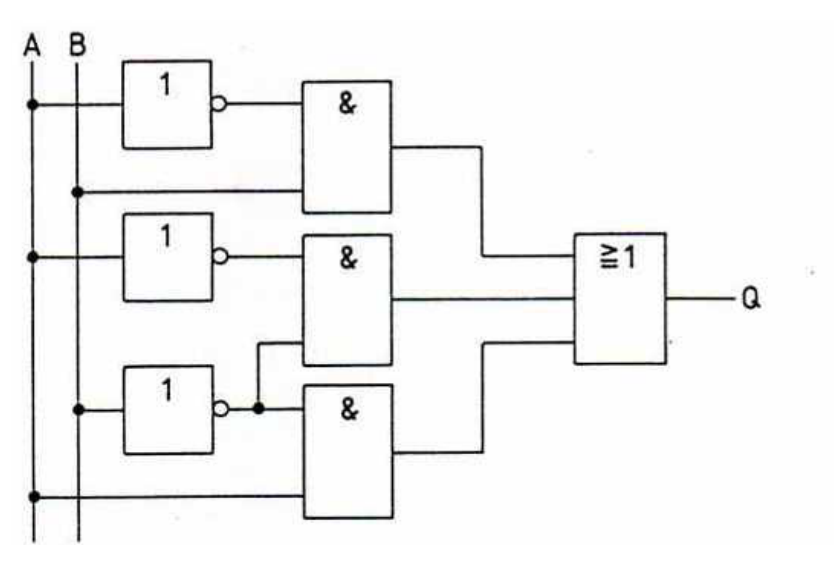
\(Q=(\overline A\land B)\lor(\overline A\land\overline B)\lor(A\land\overline B)\)
| B | A | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Vereinfachung: NICHT-UND / NAND
Schaltzeichen siehe Tabellenbuch S. 355
Aufgabe 3
Die folgende Schaltung entspricht einem Logiksymbol.
Ermittle zuerst die Funktionsgleichung, stelle dann die Wertetabelle auf und gib schlußendlich das vereinfachte Schaltzeichen (Logiksymbol) an.
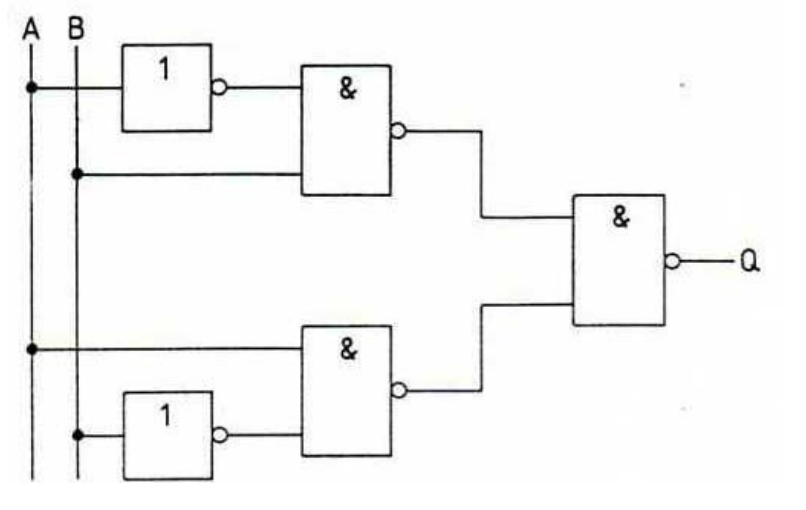
\(Q=\overline{\overline{(\overline A\land B)} \land\overline{(A\land\overline B)}}=(\overline A\overline\land\ B)\overline\land(A\overline\land\overline B)\)
| B | A | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Vereinfachung: EXKLUSIV-ODER / XOR
Schaltzeichen siehe Tabellenbuch S. 355
Weiter zur nächsten Lernaufgabe